
IBDP Maths AA Resources
Topic 1: Algebra
Exponents (Indices) and Their Properties
Exponents, also called indices or powers, describe how many times a number (the base) is multiplied by itself.
The fundamental laws of exponents include:
For any real numbers a, b and any exponents m, n:
Logarithms and Their Properties
A logarithm is the inverse operation of exponentiation:
Law of logarithms:



Arithmetic Sequences and Series
An arithmetic sequence is a sequence of numbers in which each term increases or decreases by a constant value, called the common difference (d).
An arithmetic series is the sum of the first n terms in the sequences.
Geometric Sequences and Series
A geometric sequence is a sequence where each term is obtained by multiplying the previous term by a constant called the common ratio (r).

Binomial Theorem
The Binomial Theorem provides a method to expand expressions of the form (a + b)ⁿ without direct multiplication. It is widely used in algebra, combinatorics, and probability.
The binomial expansion formula, for n ≥ 0, is
The binomial coefficient in the expansion is
The specific term in the expansion is
Note: the 5th term would translate to r = 4, instead of 5. As we count 1st term is 0, 2nd is 1, 3rd is 2, 4th is 3 and 5th is 4.
(HL only) The negative and fractional binomial expansion is
This is an infinite series, where | x | < 1.




Complex Numbers (HL Only)
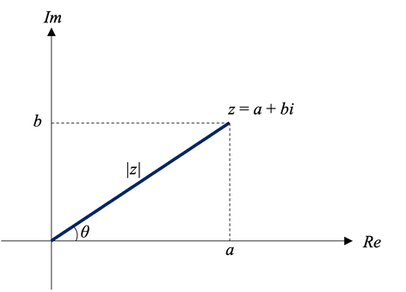
it is written in the format: z = a + bi
-
a is the real part, (Re(z))
-
b is the imaginary part, (Im(z))
-
i is the imaginary unit, i ² = – 1
(is a useless thing so people can solve something that is "unsolvable" originally)
Operations
Addition:
Subtraction:
Multiplication:
Division:
Argand Diagram (on the complex plane)
The x-axis is the real axis
The y-axis is the imaginary axis
Polar Form
z = r (cos θ + i sin θ)
where
Euler's formula
the exponential form is
De Moivre's Theorem
the n-th root of a complex number is given by:
where the roots are equally spaced around the complex plane.
Topic 2: Functions
Definitions and properties of functions
Definition of functions
A function is a mathematical rule that assigns exactly one output (y) to each input (x). This relationship is written as:
f : X → Y
where:
-
X is the domain (set of all possible inputs).
-
Y is the range (set of all possible outputs).
The function is often expressed as:
y = f (x)
Key Concept: Vertical Line Test
A graph represents a function if and only if a vertical line intersects the graph at most once.
-
✅ Valid function: A parabola y = x² passes the test.
-
❌ Not a function: A circle x² + y² = 4 fails since a vertical line intersects at two points.
Properties of Functions
-
Domain: The set of all possible input values (x).
-
Range : The set of all possible output values (y).
📌 Example:
For
-
Domain: x ≥ 0 (since square roots of negatives are undefined).
-
Range: y ≥ 0 (output is always non-negative).
✅ General Restrictions on Domains:
-
No division by zero: → Domain: x≠0x \neq 0.
-
No square roots of negatives: f(x)=x−2f(x) = \sqrt{x-2} → Domain: x≥2x \geq 2
Even and Odd Functions
Even Function:
A function is even if: f (−x) = f (x)
🖥 Graph: Symmetric about the y-axis.
Odd Function:
A function is odd if: f (−x) = − f (x)
🖥 Graph: Symmetric about the origin.
One-to-One and Many-to-One Functions
One-to-One Function (Injective):
Each input maps to exactly one unique output, and each output corresponds to only one input.
Example: f (x) = x³
-
Different x-values give different y-values.
-
Passes the horizontal line test (any horizontal line intersects at most once)
Many-to-One Function:
Different inputs can have the same output.
Example: f (x) = x²
-
f (2) = 4 and f (−2) = 4 → Many inputs give the same output.
-
Fails the horizontal line test.
Increasing, Decreasing, and Constant Functions
A function can be classified based on how it changes over its domain.
Increasing Function:
If f (a) < f (b) whenever a < b, the function is increasing.
Decreasing Function:
If f (a) > f (b) whenever a < b, the function is decreasing.
Constant Function:
If f (x) remains the same for all x, it is constant.
Periodic Functions
A function is periodic if it repeats its values at regular intervals.
f (x + T) = f (x)
where T is the period.
Example:
-
f (x) = sinx, f (x) = cosx
-
Period: 2π, meaning sin(x + 2π) = sinx.
Absolute Value Functions
The absolute value function is written as:
f (x) = | x |
-
If x ≥ 0, then f (x) = x.
-
If x < 0, then f (x) = −x.
🖥 Graph: A V-shape with a vertex at (0,0).
Summary of Function Properties

Domain, Range, and Inverse Functions
Domain of a Function
The domain of a function f(x)f(x) is the set of all possible input values xx for which f(x) is defined.
f : X → Y
where:
-
X is the domain (set of all possible inputs).
-
Y is the range (set of all possible outputs).
The function is often expressed as:
y = f (x)
Key Concept: Vertical Line Test
A graph represents a function if and only if a vertical line intersects the graph at most once.
-
✅ Valid function: A parabola y = x² passes the test.
-
❌ Not a function: A circle x² + y² = 4 fails since a vertical line intersects at two points.
Properties of Functions
-
Domain: The set of all possible input values (x).
-
Range : The set of all possible output values (y).
📌 Example:
For
-
Domain: x ≥ 0 (since square roots of negatives are undefined).
-
Range: y ≥ 0 (output is always non-negative).
✅ General Restrictions on Domains:
-
No division by zero: f(x)=1xf(x) = \frac{1}{x} → Domain: x≠0x \neq 0.
-
No square roots of negatives: f(x)=x−2f(x) = \sqrt{x-2} → Domain: x≥2x \geq 2
Even and Odd Functions
Even Function:
A function is even if: f (−x) = f (x)
🖥 Graph: Symmetric about the y-axis.
Odd Function:
A function is odd if: f (−x) = − f (x)
🖥 Graph: Symmetric about the origin.
One-to-One and Many-to-One Functions
One-to-One Function (Injective):
Each input maps to exactly one unique output, and each output corresponds to only one input.
Example: f (x) = x³
-
Different x-values give different y-values.
-
Passes the horizontal line test (any horizontal line intersects at most once)
Many-to-One Function:
Different inputs can have the same output.
Example: f (x) = x²
-
f (2) = 4 and f (−2) = 4 → Many inputs give the same output.
-
Fails the horizontal line test.
Increasing, Decreasing, and Constant Functions
A function can be classified based on how it changes over its domain.
Increasing Function:
If f (a) < f (b) whenever a < b, the function is increasing.
Decreasing Function:
If f (a) > f (b) whenever a < b, the function is decreasing.
Constant Function:
If f (x) remains the same for all x, it is constant.
Periodic Functions
A function is periodic if it repeats its values at regular intervals.
f (x + T) = f (x)
where T is the period.
Example:
-
f (x) = sinx, f (x) = cosx
-
Period: 2π, meaning sin(x + 2π) = sinx.
Absolute Value Functions
The absolute value function is written as:
f (x) = | x |
-
If x ≥ 0, then f (x) = x.
-
If x < 0, then f (x) = −x.
🖥 Graph: A V-shape with a vertex at (0,0).
Summary of Function Properties